2403. Strong connectivity
A strongly
connected component in a directed graph is a set of vertices such that there is
a path from any vertex to any other vertex in the set. Moreover, there is no larger
set with this property containing this set.
Given a directed
graph. Find the number of strongly connected components.
Input. The first line contains two integers n and m (1 ≤ n ≤ 10, 0 ≤ m ≤ 90) – the number
of vertices and edges in the graph, respectively. The next m lines describe the edges: the i-th
line contains two integers ui and vi (1 ≤ ui, vi
≤ n) – the start
and the end of the i-th edge
respectively. It is guaranteed that the graph has no loops or multiple edges.
Output. Print the
number of strongly connected components in the graph.
|
Sample
input 1 |
Sample
output 1 |
|
3 2 1 2 2 3 |
3 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
5 4 3 1 1 2 2 3 4 5 |
3 |
SOLUTION
graphs – strongly
connected components
Algorithm analysis
Find the number
of strongly connected components in the directed graph.
Example
Graphs, given in samples,
have the form:
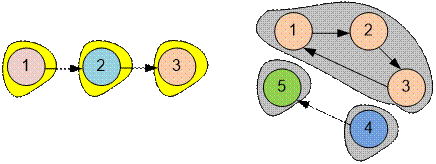
Each of these graphs has 3 strongly
connected components.
Algorithm
realization
The input graph is stored in
the adjacency list g. The inverse graph is stored in the adjacency
list gr.
vector<vector<int> > g, gr;
vector<int> used, top;
The
function dfs1 implements depth-first search on the
input graph. It adds vertices to the array top in the order in
which the depth-first search finishes processing them.
void dfs1(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs1(to);
top.push_back(v);
}
The
function dfs2 implements depth-first search on the
reversed graph. All vertices traversed during a recursive call of dfs2
belong to one strongly connected component.
void dfs2(int v)
{
used[v] = 1;
for (int to :
gr[v])
if (!used[to])
dfs2(to);
}
The
main part of the program. Read the input data. Construct the reversed graph.
scanf("%d %d", &n, &m);
g.resize(n + 1);
gr.resize(n + 1);
for(i = 1; i <= m; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
gr[b].push_back(a);
}
Run
a depth-first search on the input graph. The order in which the vertices finish
processing is stored in the top array.
used.resize(n+1);
for(i = 1; i <= n; i++)
if (!used[i])
dfs1(i);
Run
a depth-first search on the reversed graph. The
vertices of the reversed graph should be processed in the order given by
traversing the array top from right to left (from end to start). For
convenience in further processing, let’s reverse the array top.
used.clear();
used.resize(n + 1);
reverse(top.begin(),
top.end());
Use
the variable c to count the number of
strongly connected components.
c = 0;
Now move through the array top from left to right and call dfs2 from each unvisited vertex.
for (int v : top)
if (!used[v])
{
dfs2(v);
c++;
}
Print
the number of
strongly connected components in the graph.
printf("%d\n",c);
Java realization
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g, gr;
static boolean used[];
static
Vector<Integer> top = new
Vector<Integer>();
static void
dfs1(int v)
{
used[v] = true;
for(int i = 0;
i < g[v].size();
i++)
{
int to = g[v].get(i);
if (!used[to]) dfs1(to);
}
top.add(v);
}
static void
dfs2(int v)
{
used[v] = true;
for(int i = 0;
i < gr[v].size();
i++)
{
int to = gr[v].get(i);
if (!used[to]) dfs2(to);
}
}
@SuppressWarnings("unchecked")
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new
ArrayList[n+1];
for(int i = 0;
i <= n; i++)
g[i] = new
ArrayList<Integer>();
gr = new
ArrayList[n+1];
for(int i = 0;
i <= n; i++)
gr[i] = new
ArrayList<Integer>();
for (int i = 0;
i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new boolean[n+1];
for(int i = 1;
i <= n; i++)
if (!used[i]) dfs1(i);
used = new boolean[n+1];
int c = 0;
for(int i = 1;
i <= n; i++)
{
int v = top.get(n-i);
if (!used[v])
{
dfs2(v);
c++;
}
}
System.out.println(c);
con.close();
}
}
Python realization
The
function dfs1 implements depth-first search on the
input graph. It adds vertices to the array top in the order in
which the depth-first search finishes processing them.
def dfs1(v):
global g, used,
top
used[v] = True
for
to in g[v]:
if not used[to]:
dfs1(to)
top.append(v)
The
function dfs2 implements depth-first search on the
reversed graph. All vertices traversed during a recursive call of dfs2
belong to one strongly connected component.
def dfs2(v):
global gr, used
used[v] = True
for
to in gr[v]:
if not used[to]:
dfs2(to)
The
main part of the program. Read the input data. Construct the reversed graph.
n, m = map(int, input().split())
g = [[] for _ in range(n + 1)]
gr = [[] for _ in range(n + 1)]
for _ in range(m):
a,
b = map(int, input().split())
g[a].append(b)
gr[b].append(a)
Run
a depth-first search on the input graph. The order in which the vertices finish
processing is stored in the top array.
used = [False] * (n + 1)
top = []
for i in range(1, n + 1):
if not used[i]:
dfs1(i)
Run
a depth-first search on the reversed graph. The vertices of the reversed graph
should be processed in the order given by traversing the array top from
right to left (from end to start). For convenience in further processing, let’s
reverse the array top.
used = [False] * (n + 1)
top.reverse()
Use
the variable c to count the number of
strongly connected components.
c = 0
Now move through the array top from left to right and call dfs2 from each unvisited vertex.
for v in top:
if not used[v]:
dfs2(v)
c += 1
Print
the number of
strongly connected components in the graph.
print(c)